정렬(Sort)
- 특정한 값을 기준으로 데이터를 순서대로 배치하는 방법을 말한다.
- 구현 난이도는 쉽지만, 속도는 느린 알고리즘
- 버블 정렬, 삽입 정렬, 선택 정렬
- 구현 난이도는 조금 더 어렵지만, 속도는 빠른 알고리즘
- 합병 정렬, 힙 정렬, 퀵 정렬, 트리 정렬
- 하이브리드 정렬
- 팀 정렬, 블록 병합 정렬, 인트로 정렬
- 기타 정렬 알고리즘
- 기수 정렬, 카운팅 정렬, 셸 정렬, 보고 정렬
버블 정렬(Bubble Sort)
버블 정렬(Bubble Sort)는 인접한 두 개의 요소를 비교하면서 정렬하는 알고리즘이다. 두 개의 요소를 비교하면서 더 작은 값을 앞으로 이동시키고, 큰 값을 뒤로 이동시키는 방식으로 정렬을 수행한다. 이를 배열 끝까지 반복하면서 정렬을 완성한다. 이러한 정렬되는 모습이 거품이 수면위로 올라오는 것과 비슷하다고 하여 버블 정렬이라고 불린다.
버블 정렬은 구현이 쉽지만, 배열의 크기가 클수록 비효율적인 알고리즘이기 때문에 대부분의 경우 다른 정렬 알고리즘보다 느리다. 최선의 경우 시간 복잡도는 O(n)이지만, 평균과 최악의 경우 시간 복잡도는 O(n^2)이다. 따라서, 큰 데이터를 정렬할 때는 다른 알고리즘을 사용하는 것이 좋다.

코드
public void bubbleSort(int[] arr) {
for(int i = 1; i < arr.length -1 ; i++){
for(int j = 0; j < arr.length - i; j++){
if(arr[j] > arr[j+1]) swap(arr, j, j + 1); // 왼쪽값이 오른쪽보다 크면 자리 변경
}
}
}삽입 정렬(Insertion Sort)
삽입 정렬(Insertion Sort)은 각 요소를 적절한 위치에 삽입하면서 정렬하는 알고리즘이다. 이 알고리즘은 선택 정렬(Selection Sort)와 유사하지만, 선택 정렬은 가장 작은 값을 찾아서 맨 앞으로 이동시키는 반면에 삽입 정렬은 각 요소를 삽입하여 정렬한다.
삽입 정렬의 시간 복잡도는 평균적으로 O(n^2)이다. 최선의 경우(이미 정렬된 경우)는 O(n)이며, 최악의 경우(역순으로 정렬된 경우)는 O(n^2)이다. 따라서, 큰 데이터를 정렬할 때는 다른 알고리즘을 사용하는 것이 이다. 그러나, 데이터가 적을 때는 다른 알고리즘보다 성능이 우수하며, 안정적인 알고리즘이다.

코드
public void insertionSort(int[] arr) {
for(int i = 1; i < arr.length ; i++){
for(int j = i; j >= 0 ; j--){
if(arr[j] < arr[j-1]) swap(arr, j, j - 1); // 왼쪽값이 오른쪽보다 크면 자리 변경
}
}
}선택 정렬(Selection Sort)
선택 정렬(Selection Sort)은 주어진 리스트에서 최소값을 찾고 그 값을 맨 앞에 위치한 값과 교체하며, 맨 처음 위치를 뺀 나머지 리스트를 대상으로 위의 과정을 반복하여 정렬하는 알고리즘이다.

선택 정렬은 단순하지만, 비효율적인 알고리즘이다. 이유는, n개의 데이터를 정렬하는 경우, 비교 연산이 n-1 + n-2 + ... + 1 = (n^2 - n) / 2 번 수행되기 때문이다. 즉, 시간 복잡도는 O(n^2)이다. 따라서, 대부분의 경우 다른 정렬 알고리즘보다 느리다.
하지만 선택 정렬은 자료 이동 횟수가 미리 결정되어 있어서, 자료 이동 횟수가 많은 경우에는 다른 정렬 알고리즘보다 효율적일 수 있다. 또한, 정렬 중간 상태도 유지되기 때문에 안정성을 보장한다.
코드
public void selectionSort(int[] arr) {
for(int i = 0; i < arr.length - 1 ; i++){
int min = 0;
for(int j = i + 1; j <= arr.length - 1; j++){
if(arr[min] > arr[j]) min = j; // 배열내에 min index 값보다 작은값이 존재 할 경우
}
swap(arr, i, min); // min과 i인덱스 값을 변경함.
}
}합병 정렬(Merge Sort)
합병 정렬(Merge Sort)은 분할 정복(Divide and Conquer) 알고리즘을 사용하여 리스트를 정렬하는 알고리즘이다. 합병 정렬은 일반적으로 O(nlogn) 시간 복잡도를 가지므로 대부분의 정렬 문제에서 성능이 우수한 알고리즘 중 하나이다.
합병 정렬은 재귀적으로 문제를 해결하기 때문에, 스택 메모리를 많이 사용할 수 있다. 하지만, 합병 정렬은 안정적인 정렬 알고리즘이기 때문에, 정렬 중 순서가 같은 값이 있을 경우에도 정렬 순서가 유지된다.

코드
public static void mergeSort(int[] arr, int[] tmp, int left, int right) {
if (left < right) {
int mid = (left + right) / 2;
mergeSort(arr, tmp, left, mid);
mergeSort(arr, tmp, mid + 1, right);
merge(arr, tmp, left, right, mid);
}
}
public static void merge(int[] arr, int[] tmp, int left, int right, int mid) {
int p = left;
int q = mid + 1;
int idx = p;
// p, q 둘 중 하나는 해당 배열 범위 안에 있는 동안
while (p <= mid || q <= right) {
if (p <= mid && q <= right) { // 둘 다 범위 안인 경우
if (arr[p] <= arr[q]) { // 값 비교하여 정렬
tmp[idx++] = arr[p++];
} else {
tmp[idx++] = arr[q++];
}
} else if (p <= mid && q > right) { // 왼쪽만 남은 경우 이어주기
tmp[idx++] = arr[p++];
} else { // 오른쪽만 남은 경우 이어주기
tmp[idx++] = arr[q++];
}
}
for (int i = left; i <= right; i++) { // 정렬된 부분 데이터 arr 쪽으로
arr[i] = tmp[i];
}
}힙 정렬(Heap Sort)
힙 정렬(Heap Sort)은 힙(Heap) 자료구조를 이용하여 리스트를 정렬하는 알고리즘이다. 힙 정렬은 일반적으로 O(nlogn) 시간 복잡도를 가지므로 대부분의 정렬 문제에서 성능이 우수한 알고리즘 중 하나이다.
힙 자료구조는 완전 이진트리로 구성된 자료구조로, 최대 힙(Max Heap)과 최소 힙(Min Heap) 두 가지 종류가 있다. 최대 힙은 부모 노드의 값이 자식 노드의 값보다 큰 완전 이진트리이며, 최소 힙은 부모 노드의 값이 자식 노드의 값보다 작은 완전 이진트리이다.
힙 정렬의 장점은 추가적인 메모리 공간을 필요로 하지 않는다는 것이다. 힙 정렬은 또한 데이터가 무작위로 분포되어 있을 때도 빠른 정렬 속도를 보인다. 그러나 힙 정렬은 데이터가 거의 정렬된 경우에는 다른 정렬 알고리즘에 비해 상대적으로 느리게 동작할 수 있다. 또한, 알고리즘이 구현하기 복잡하고, 일반적으로 다른 정렬 알리즘들보다는 느리지만, 최악의 경우에도 O(nlogn)의 시간복잡도를 보장하는 안정적인 알고리즘이다.
힙 정렬은 다른 정렬 알고리즘들과 마찬가지로 안정적인 알고리즘은 아니다. 따라서 입력 데이터의 순서에 따라서 결과가 바뀔 수 있다. 힙 정렬은 대부분의 경우에 사용할 수 있는 제네릭한 정렬 알고리즘이다. 즉, 정수, 문자열, 객체 등 모든 종류의 데이터 타입에 대해서도 사용할 수 있다. 이러한 이유로 힙 정렬은 대부분의 프로그래밍 언어에서 기본으로 제공하는 정렬 알고리즘 중 하나이다.
코드
public static void heapSort(int[] arr) {
// 힙으로 재구성 (maxHeap 기준, 마지막 부모 노드부터)
for(int i = arr.length / 2 - 1; i >= 0; i--) {
heapify(arr, i, arr.length);
}
// maxHeap 기준 root 쪽을 끝 쪽으로 보내면서 재정렬 -> 오름차순
for(int i = arr.length - 1; i > 0; i--) {
swap(arr, 0, i);
heapify(arr, 0, i);
}
}
public static void heapify(int[] arr, int parentIdx, int size) {
// 자식 노드 위치
int leftIdx = 2 * parentIdx + 1;
int rightIdx = 2 * parentIdx + 2;
int maxIdx = parentIdx;
// 왼쪽 자식 노드가 크면 maxIdx 를 해당 인덱스로 교체
if(leftIdx < size && arr[maxIdx] < arr[leftIdx]) {
maxIdx = leftIdx;
}
// 오른쪽 자식 노드가 크면 maxIdx 를 해당 인덱스로 교체
if(rightIdx < size && arr[maxIdx] < arr[rightIdx]) {
maxIdx = rightIdx;
}
// maxIdx 가 바뀐 경우, 부모 노드가 교체되는 것을 의미
// 교체하고 서브 트리 검사 하도록 재귀 호출
if(parentIdx != maxIdx) {
swap(arr, maxIdx, parentIdx);
heapify(arr, maxIdx, size);
}
}
public static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}퀵 정렬(Quick Sort)
퀵 정렬(Quick Sort)은 대표적인 분할 정복(Divide and Conquer) 알고리즘 중 하나로, 평균적으로 O(nlogn)의 시간 복잡도를 가지면서, 매우 빠른 정렬 알고리즘으로 알려져 있다.
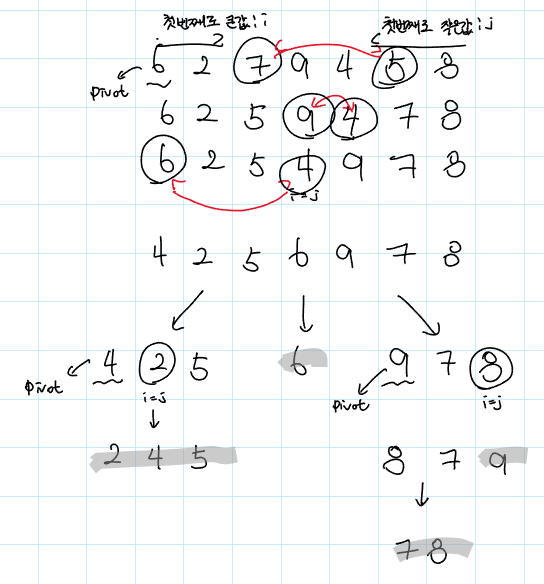
퀵 정렬은 배열을 분할하고, 각 분할된 배열을 재귀적으로 정렬하는 방식으로 동작한다. 분할(Divide) 과정에서는 배열에서 하나의 피벗(pivot) 값을 선택한 후, 피벗 값보다 작은 원소는 피벗의 왼쪽으로, 큰 원소는 피벗의 오른쪽으로 나눈다. 이후 분할된 배열을 각각 다시 정렬한다.
퀵 정렬의 시간 복잡도는 대부분의 경우에 O(nlogn)이다. 퀵 정렬의 평균 시간 복잡도는 O(nlogn)이지만, 피벗의 선택에 따라서 최악의 경우 O(n^2)의 시간 복잡도를 가질 수도 있다. 따라서 피벗의 선택이 매우 중요하다. 일반적으로는 중앙값을 선택하거나, 랜덤하게 선택하는 방식으로 최악의 경우를 피하려고 한다. 그리고 퀵 정렬은 안정적인 정렬 알고리즘이 아니다. 즉, 입력 데이터의 순서에 따라서 결과가 바뀔 수 있다.
코드
public static void quickSort(int[] arr, int left, int right) {
if(left >= right) {
return;
}
// 분할
int pivot = partition(arr, left, right);
// 기준값 중심으로 좌우 재귀 호출
quickSort(arr, left, pivot - 1);
quickSort(arr, pivot + 1, right);
}
public static int partition(int[] arr, int left, int right) {
// 가장 좌측 값을 기준값으로 설정
// 이외에 기준 값은 배열에서 중간에 있는 값을 고르거나, 임의의 수를 3개 선정 후 중앙 값을 고르는 등의 방법이 있음
int pivot = arr[left];
int i = left;
int j = right;
while(i < j) {
while (arr[j] > pivot && i < j) {
j--;
}
while(arr[i] <= pivot && i < j) {
i++;
}
swap(arr, i, j);
}
swap(arr, left, i);
return i;
}
public static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}트리 정렬(Tree Sort)
트리 정렬(Tree Sort)은 이진 탐색 트리(Binary Search Tree)를 이용한 정렬 알고리즘 중 하나이다. 이진 탐색 트리는 모든 노드의 왼쪽 서브 트리의 값이 해당 노드의 값보다 작고, 오른쪽 서브 트리의 값이 해당 노드의 값보다 큰 트리이다.
트리 정렬은 입력 데이터의 크기가 작을 때는 효율적인 알고리즘이지만, 입력 데이터가 많아질수록 효율이 떨어진다. 이는 이진 탐색 트리에 삽입하는 과정에서 평균적으로 O(log n)의 시간 복잡도를 가지기 때문이다. 따라서 입력 데이터가 많은 경우에는 다른 정렬 알고리즘을 사용하는 것이 좋다.
또한, 이진 탐색 트리를 구현할 때, 균형잡힌 트리(Balanced Tree)를 사용하는 것이 중요하다. 이는 이진 탐색 트리의 높이를 최소화하여 삽입, 삭제, 탐색 연산을 더 빠르게 수행할 수 있도록 한다. 대표적으로 AVL 트리, 레드-블랙 트리 등이 있다.
따라서, 트리 정렬은 입력 데이터가 적은 경우에는 빠른 속도를 보여주지만, 입력 데이터가 많은 경우에는 다른 정렬 알고리즘을 사용하는 것이 좋다.
이진 탐색 트리(Binary Search Tree)
이진 탐색 트리(Binary Search Tree) 이진트리는 아래의 규칙을 가지고 있는 자료구조이다. 왼쪽 자식 노드의 키는 부모 노드의 키보다 작다. 오른쪽 자식 노드의 키는 부모 노드의 키보다 크다. 각각
jamesblog95.tistory.com
기수 정렬(Radix Sort)
기수 정렬(Radix Sort)은 비교 기반 정렬 알고리즘이 아니며, 자릿수를 이용한 정렬 알고리즘이다. 주로 정수나 문자열과 같은 자료형에서 사용된다.
기수 정렬은 자릿수마다 버킷을 만들어야 하므로, 메모리를 많이 사용할 수 있다. 또한, 입력 데이터의 자릿수가 많아질수록 정렬 시간이 늘어나게 된다. 따라서, 입력 데이터의 자릿수가 많은 경우에는 다른 정렬 알고리즘을 사용하는 것이 좋다.
하지만, 기수 정렬은 안정성을 보장하며, 어떠한 상황에서도 최악의 경우 O(nk)의 시간 복잡도를 가진다. (n은 입력 데이터의 개수, k는 자릿수의 개수) 따라서, 입력 데이터의 자릿수가 많지 않은 경우에는 퀵 정렬과 같은 비교 기반 정렬 알고리즘보다 빠른 속도를 보여줄 수 있다.

코드
public static void radixSort(int[] arr) {
// 기수 테이블 생성
ArrayList<Queue<Integer>> list = new ArrayList<>();
for (int i = 0; i < 10; i++)
{
list.add(new LinkedList());
}
int idx = 0;
int div = 1;
int maxLen = getMaxLen(arr);
// 자리수 만큼 기수 정렬 반복
for (int i = 0; i < maxLen; i++)
{
// 각 자리수에 맞는 큐 위치에 데이터 삽입
for (int j = 0; j < arr.length; j++) {
list.get((arr[j] / div) % 10).offer(arr[j]);
}
// 다시 순서대로 가져와서 배치
for (int j = 0; j < 10; j++) {
Queue<Integer> queue = list.get(j);
while (!queue.isEmpty()) {
arr[idx++] = queue.poll();
}
}
idx = 0;
div *= 10;
}
}
public static int getMaxLen(int[] arr)
{
// 배열에 숫자들 중 가장 긴 자리수 구하기
int maxLen = 0;
for (int i = 0; i < arr.length; i++) {
int len = (int)Math.log10(arr[i]) + 1;
if (maxLen < len) {
maxLen = len;
}
}
return maxLen;
}계수 정렬(Counting Sort)
계수 정렬(Counting Sort)은 비교 기반 정렬 알고리즘이 아니며, 입력 데이터의 범위가 제한된 경우에 사용된다. 예를 들어, 0 이상 k 이하의 자연수로 이루어진 입력 데이터를 정렬하는 경우, 계수 정렬을 사용할 수 있다.
계수 정렬은 입력 데이터의 범위가 크지 않은 경우에는 매우 빠른 속도를 보여줄 수 있다. 시간 복잡도는 O(n+k)이며, 입력 데이터의 범위가 크지 않은 경우에는 다른 비교 기반 정렬 알고리즘보다 빠른 속도를 보여줄 수 있다. 하지만, 입력 데이터의 범위가 매우 큰 경우에는 메모리를 많이 사용하게 되어 사용이 어려울 수 있다. 또한, 계수 정렬은 안정적인 정렬 알고리즘이며, 입력 데이터의 값이 중복되는 경우에도 정확하게 정렬된다.

코드
public static void countingSort(int[] arr) {
// # 1 일반 배열 사용
// 최대값 구해서 배열 설정
int max = Arrays.stream(arr).max().getAsInt();
int[] cntArr = new int[max + 1];
for (int i = 0; i < arr.length; i++) {
cntArr[arr[i]]++;
}
int idx = 0;
for (int i = 0; i < cntArr.length; i++) {
while (cntArr[i] > 0) {
arr[idx++] = i;
cntArr[i] -= 1;
}
}
// # 2 Hashmap 사용
HashMap<Integer, Integer> map = new HashMap<>();
for (int item: arr) {
map.put(item, map.getOrDefault(item, 0) + 1);
}
int idx2 = 0;
ArrayList<Integer> list = new ArrayList(map.keySet());
Collections.sort(list);
for (int i = 0; i < list.size(); i++) {
int cnt = map.get(list.get(i));
while (cnt > 0) {
arr[idx2++] = list.get(i);
cnt--;
}
}
}셸 정렬(Shell Sort)
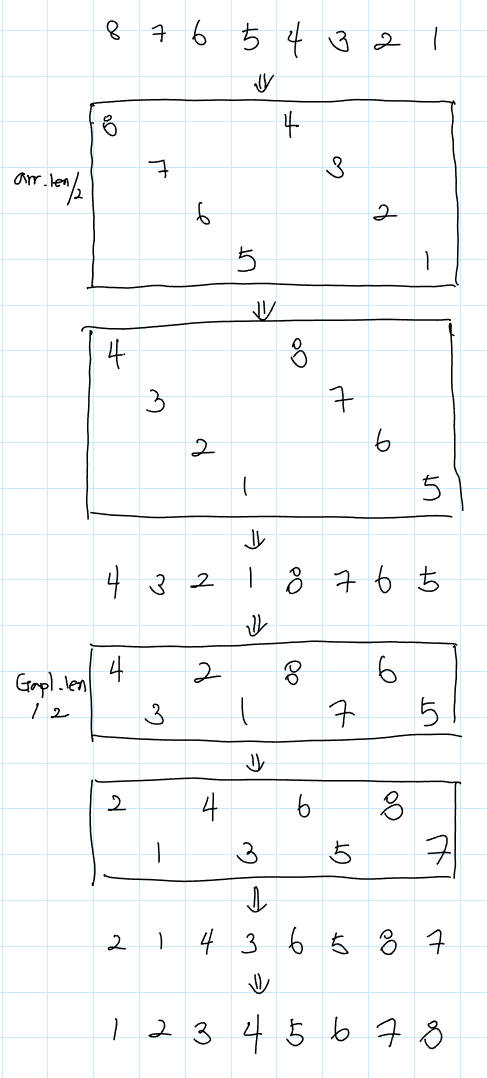
셸 정렬(Shell Sort)은 삽입 정렬을 보완하여 만들어진 정렬 알고리즘이다. 삽입 정렬과 마찬가지로 원소를 하나씩 비교하면서 삽입하면서 정렬을 수행하는 알고리즘이다. 하지만 삽입 정렬과 달리 셸 정렬은 먼 거리에 있는 원소들끼리 비교하면서 삽입을 수행한다.
셸 정렬은 삽입 정렬과 비교하여 간격 h가 있어서 전체 리스트를 한 번에 정렬하지 않고 부분 리스트를 먼저 정렬하는 것이 특징이다. 이로 인해, 삽입 정렬보다 더욱 빠른 속도를 보일 수 있다.
코드
public static void shellSort(int[] arr) {
// 초기 간격
int gap = arr.length / 2;
// 초기 간격부터 간격 반씩 줄여가면서 진행
for (int g = gap; g > 0; g /= 2) {
for (int i = g; i < arr.length; i++) {
int tmp = arr[i];
int j = 0;
for (j = i - g; j >= 0; j -= g) {
if (arr[j] > tmp) {
arr[j + g] = arr[j];
} else {
break;
}
}
arr[j + g] = tmp;
}
}
}'Zero-Base > 자료구조-알고리즘' 카테고리의 다른 글
| 투 포인터, 그리디 (0) | 2023.04.01 |
|---|---|
| 이진탐색(Binary Search) (0) | 2023.04.01 |
| 우선순위 큐(Priority Queue), 트라이(Trie) (0) | 2023.03.29 |
| 그래프(Graph) (0) | 2023.03.28 |
| AVL, Red-Black Tree (0) | 2023.03.28 |

