문제
간선에 가중치와 방향성이 없는 임의의 루트 있는 트리가 주어졌을 때, 아래의 쿼리에 답해보도록 하자.
- 정점 U를 루트로 하는 서브트리에 속한 정점의 수를 출력한다.
만약 이 문제를 해결하는 데에 어려움이 있다면, 하단의 힌트에 첨부한 문서를 참고하자.
입력
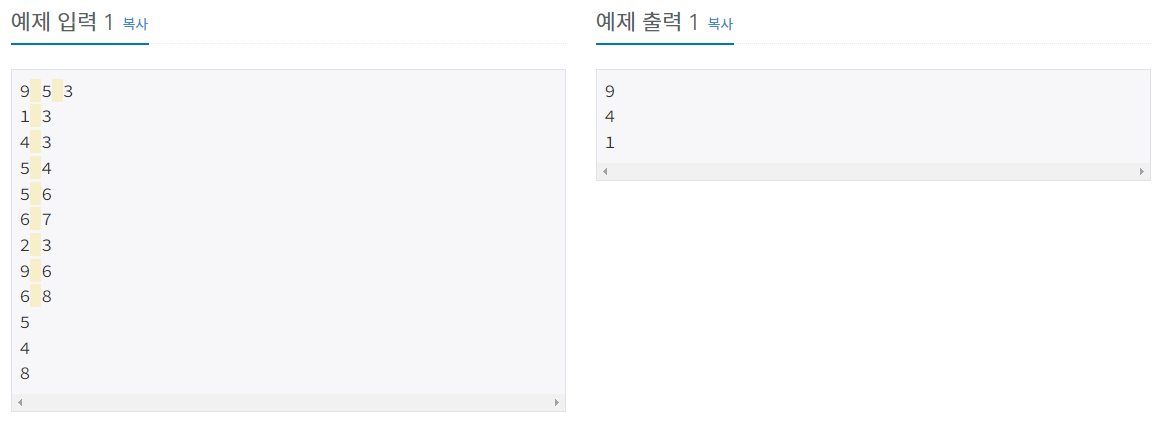
트리의 정점의 수 N과 루트의 번호 R, 쿼리의 수 Q가 주어진다. (2 ≤ N ≤ 105, 1 ≤ R ≤ N, 1 ≤ Q ≤ 105)
이어 N-1줄에 걸쳐, U V의 형태로 트리에 속한 간선의 정보가 주어진다. (1 ≤ U, V ≤ N, U ≠ V)
이는 U와 V를 양 끝점으로 하는 간선이 트리에 속함을 의미한다.
이어 Q줄에 걸쳐, 문제에 설명한 U가 하나씩 주어진다. (1 ≤ U ≤ N)
입력으로 주어지는 트리는 항상 올바른 트리임이 보장된다.
출력
Q줄에 걸쳐 각 쿼리의 답을 정수 하나로 출력한다.
문제 풀이
해당 문제는 트리 자료구조로 풀 수 있는 문제이다.
각 노드가 가지고 있는 하위 노드의 수를 반환해야 하는 문제이므로 우선 트리를 구성해야 한다. 예제 1번을 기준으로 트리를 구성하면 아래와 같은 모습을 띈다.

이 후 입력이 되는 쿼리를 기준으로 5번 노드는 root 노드로 총 9개의 본인을 포함한 하위 노드를 가지고 있다. 그리고 4는 4개, 8은 1개로 쿼리에 맞게 출력해주면 된다.
나의 답안
import java.io.IOException;
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
public class Main {
static List<Integer>[] graph;
static boolean[] visited;
static int[] subTree;
public static void main(String[] args) throws IOException {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int r = sc.nextInt();
int q = sc.nextInt();
graph = new ArrayList[n + 1];
visited = new boolean[n + 1];
subTree = new int[n + 1];
for (int i = 0; i < n + 1; i++) {
graph[i] = new ArrayList<>();
}
for (int i = 0; i < n - 1; i++) {
int u = sc.nextInt();
int v = sc.nextInt();
graph[u].add(v);
graph[v].add(u);
}
dfs(r);
for (int i = 0; i < q; i++) {
System.out.println(subTree[sc.nextInt()]);
}
}
private static void dfs(int node) {
visited[node] = true;
subTree[node] = 1;
for (int next : graph[node]) {
if (!visited[next]) {
dfs(next);
subTree[node] += subTree[next];
}
}
}
}
'BackJoon > Algorithm' 카테고리의 다른 글
| (11726) 2*n 거리 (0) | 2023.04.21 |
|---|---|
| (1240) 노드사이의 거리 (0) | 2023.04.19 |
| (4803) 트리 (0) | 2023.04.19 |
| (1991) 트리 순회 (0) | 2023.04.19 |
| (11725) 트리의 부모 찾기 (0) | 2023.04.19 |

