문제
문제
N-Queen 문제는 크기가 N × N인 체스판 위에 퀸 N개를 서로 공격할 수 없게 놓는 문제이다.N이 주어졌을 때, 퀸을 놓는 방법의 수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 N이 주어진다. (1 ≤ N < 15)
출력
첫째 줄에 퀸 N개를 서로 공격할 수 없게 놓는 경우의 수를 출력한다.
문제 풀이
해당 문제는 백트래킹 알고리즘으로 해결 할 수 있는 문제이다. 문제에 앞서 체스판에서 퀸은 가로, 세로, 대각선을 모두 움직일 수 있는 말이라는 것을 알고 있어야 문제를 이해가능하다.

그렇다면 하나의 퀸을 두고, 다른 퀸을 두려고 하면 같은 대각선인지, 같은 열과 행인지를 검사하면 된다. 기본적으로 row의 경우에는 재귀함수를 통해 매번 새로운 값으로 비교를 하니 문제는 없다. 그렇다면 비교해야 하는 것은 column과 대각선이다.
여기서 우리가 col은 배열로 구현을 하여서 처리를 할 수 있지만 대각선은 어떻게 처리해야 되는지 고민을 해야한다. 먼저 대각선의 특성을 보자면 절대값(row - col)을 하면 해당 대각선의 값을 알 수 있다.
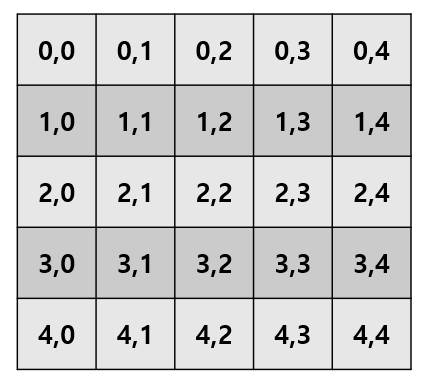
여기서 Math.abs(x1 - x2) = y1 + y2 라는 공식이 성립하면 같은 대각선에 있다는 것을 알 수 있다.
나의 답안
public class Main {
static int n;
static int[] cols;
static int count = 0;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
n = Integer.parseInt(br.readLine());
cols = new int[n];
backtracking(0);
System.out.println(count);
}
static void backtracking(int row) {
if (row == n) {
count++;
return;
}
for (int i = 0; i < n; i++) {
cols[row] = i;
if (isPossible(row)){
backtracking(row + 1);
}
}
}
static boolean isPossible(int row) {
for (int i = 0; i < row; i++) {
if (cols[i] == cols[row] || Math.abs(cols[row] - cols[i]) == row - i) return false;
}
return true;
}
}
'BackJoon > Algorithm' 카테고리의 다른 글
| (14888) 연산자 끼워넣기 (1) | 2023.04.10 |
|---|---|
| (15651) N과 M(3) (0) | 2023.04.10 |
| (15650) N 과 M(2) (0) | 2023.04.10 |
| (15649) N과 M(1) (0) | 2023.04.10 |
| (11727)2xn 타일링 2 (0) | 2023.04.09 |


