문제
한수는 크기가 2N × 2N인 2차원 배열을 Z모양으로 탐색하려고 한다. 예를 들어, 2×2배열을 왼쪽 위칸, 오른쪽 위칸, 왼쪽 아래칸, 오른쪽 아래칸 순서대로 방문하면 Z모양이다.

N > 1인 경우, 배열을 크기가 2N-1 × 2N-1로 4등분 한 후에 재귀적으로 순서대로 방문한다.
다음 예는 22 × 22 크기의 배열을 방문한 순서이다.
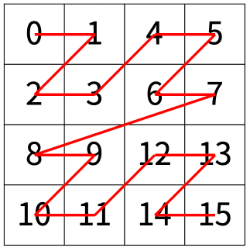
N이 주어졌을 때, r행 c열을 몇 번째로 방문하는지 출력하는 프로그램을 작성하시오.
다음은 N=3일 때의 예이다.

입력
첫째 줄에 정수 N, r, c가 주어진다.
출력
r행 c열을 몇 번째로 방문했는지 출력한다.
제한
- 1 ≤ N ≤ 15
- 0 ≤ r, c < 2N
문제풀이
해당 문제는 분할정복 알고리즘으로 해결 할 수 있는 문제이다.
기본적인 분할정복문제로 2차원 배열을 만들어서 값을 계산하고 해당 위치에 있는 방식으로 초반에 접근 하였지만 시간초과로 인해 실패 했다.
이후 방식으로는 해당 r, c 값에 바로 찾아서 계산하는 방법을 사용을 하여 풀었으며 아래와 같은 방법을 사용하였다.
좌표의 시작점 x, y 그리고 현재 배열의 사이즈를 나타내는 size를 사용해서 배열을 표시하고 있다.

r, c 에 알맞는 값을 찾기 위해서는 현재 x, y 두 개 다 증가해야 하는데, 현재 위치에서는 4등분 나눈 블록에서 3번째 블록으로 이동해야 한다.
이동하는 과정에서 result 값에 값을 더해주어서 현재 위치인 8로 만들어 주어야 한다.

다시 한번 더 원하는 값을 찾기 위해서는 8 ~ 11 사이의 블록에서 마지막 11번 블록으로 가야 하는데 이 때 size가 1이 되면 result를 증가시켜주는 계산을 하도록 하여 11을 만들어 주면 된다.

x, y 가 r, c 와 같아 졌을때 현재 result 값을 출력한다.
나의 답안
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
public class Main {
static int N, r, c, result;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
r = Integer.parseInt(st.nextToken());
c = Integer.parseInt(st.nextToken());
result = 0;
int size = (int) Math.pow(2, N);
find(0, 0, size);
}
private static void find(int x, int y, int size) {
if (size == 1) {
if (x == r && y == c) System.out.println(result);
result++;
return;
}
int nSize = size / 2;
int num = nSize * nSize;
if (r < nSize + x && c < nSize + y) {
find(x, y, nSize);
} else if (r < nSize + x && c >= nSize + y) {
result += num;
find(x, y + nSize, nSize);
} else if (r >= nSize + x && c < nSize + y) {
result += num * 2;
find(x + nSize, y, nSize);
} else {
result += num * 3;
find(x + nSize, y + nSize, nSize);
}
}
}'BackJoon > Algorithm' 카테고리의 다른 글
| (1107) 리모컨 (0) | 2023.04.30 |
|---|---|
| (1759) 암호 만들기 (0) | 2023.04.30 |
| (2805) 나무 자르기 (0) | 2023.04.30 |
| (1351) 무한 수열 (0) | 2023.04.27 |
| (2293) 동전 1 (1) | 2023.04.22 |

