문제
수열 A가 주어졌을 때, 가장 긴 증가하는 부분 수열을 구하는 프로그램을 작성하시오.
예를 들어, 수열 A = {10, 20, 10, 30, 20, 50} 인 경우에 가장 긴 증가하는 부분 수열은 A = {10, 20, 10, 30, 20, 50} 이고, 길이는 4이다.
입력
첫째 줄에 수열 A의 크기 N (1 ≤ N ≤ 1,000)이 주어진다.
둘째 줄에는 수열 A를 이루고 있는 Ai가 주어진다. (1 ≤ Ai ≤ 1,000)
출력
첫째 줄에 수열 A의 가장 긴 증가하는 부분 수열의 길이를 출력한다.
둘째 줄에는 가장 긴 증가하는 부분 수열을 출력한다. 그러한 수열이 여러가지인 경우 아무거나 출력한다.

문제 풀이
해당 문제는 DP 알고리즘으로 풀 수 있는 문제이다.
먼저 배열에 있는 값중에서 가장 긴 증가를 하는 부분 수열을 구하는 문제이다. 해당 문제에서 알아 둬야 하는 것은 꼭 index 0번이 제일 작은 값이 아닌경우의 subproblem을 파악하여 해결 하도록 만들어야 하는게 중요하다.
배열에 아래와 같이 입력 되어 있다고 하면 제일 긴 배열의 값은 10 ~ 60 까지 이다.

먼저 배열의 길이를 저장 하는 int[] dp = new int[n]을 만들어 준다.
그리고 제일 긴 값을 반환하는 int len = 1을 선언 해준다.
그리고 index i 기준으로 i 미만의 index에 있는 배열에서 작은 값이 존재한다면 해당 값의 dp[j] 에 +1을 해주고 dp[i] 에 입력 해주게 되면 현재 index i 값은 작은 값 대비 + 1 큰 값은 가지게 된다.
위에 말을 수식으로 정리하면 이러하다. dp[i] = dp[j] + 1
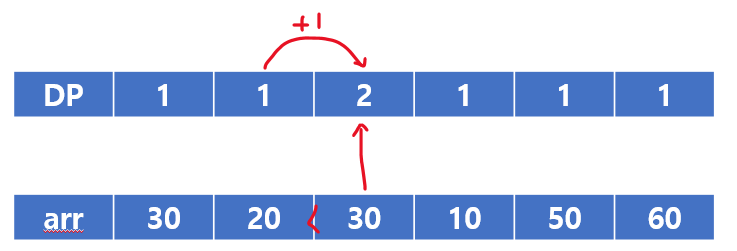
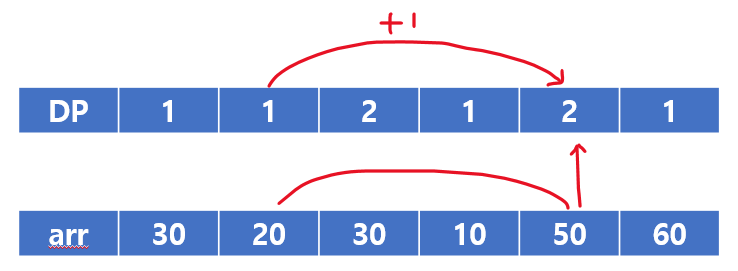

배열 마지막 60은 바로 앞에 있는 50보다 크므로 dp 값은 4로 되고 len도 4가 된다.
이후 역탐색으로 값을 추출하면 끝이다.
나의 답안
import java.util.*;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int[] arr = new int[n + 1];
int[] dp = new int[n + 1];
for (int i = 1; i <= n ; i++) {
arr[i] = scanner.nextInt();
}
dp[1] = 1;
int len = 1;
for (int i = 2; i <= n ; i++) {
dp[i] = 1;
for (int j = 1; j < i; j++) {
if (arr[i] > arr[j] && dp[i] <= dp[j]){
dp[i] = dp[j] + 1;
}
}
len = Math.max(len, dp[i]);
}
int v = len;
Stack<Integer> stack = new Stack<>();
for (int i = n; i >= 1 ; i--) {
if (v == dp[i]) {
stack.push(arr[i]);
v--;
}
}
StringBuilder sb = new StringBuilder();
System.out.println(len);
while (!stack.isEmpty()){
sb.append(stack.pop() + " ");
}
System.out.println(sb.toString());
}
}'BackJoon > Algorithm' 카테고리의 다른 글
| (1351) 무한 수열 (0) | 2023.04.27 |
|---|---|
| (2293) 동전 1 (1) | 2023.04.22 |
| (2579) 계단 오르기 (0) | 2023.04.21 |
| (11726) 2*n 거리 (0) | 2023.04.21 |
| (1240) 노드사이의 거리 (0) | 2023.04.19 |

