문제
문제
정수 4를 1, 2, 3의 합으로 나타내는 방법은 총 7가지가 있다. 합을 나타낼 때는 수를 1개 이상 사용해야 한다.1+1+1+11+1+21+2+12+1+12+21+33+1정수 n이 주어졌을 때, n을 1, 2, 3의 합으로 나타내는 방법의 수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스는 한 줄로 이루어져 있고, 정수 n이 주어진다. n은 양수이며 11보다 작다.
출력
각 테스트 케이스마다, n을 1, 2, 3의 합으로 나타내는 방법의 수를 출력한다.
문제 풀이
해당 문제는 DP로 해결 할 수 있는 문제이다. 이전의 값들의 경우의 수를 기억해서 다음 수에는 해당 값들을 더해주면 되는 문제이다.
1을 만들 수 있는 경우의 수는 1이다.
2를 만들 수 있는 경우의 수는 2이다.
3을 만들 수 있는 경우의 수는 4이다.
4를 만들 수 있는 경우의 수는 7이다.
이렇게 나열하고 보면 규칙이 보이는데 바로 현재의 값의 경우의 수는 이전 3개의 경우의 수를 총 합과 같다는 것이다. 이러한 방식을 적용하여 문제를 풀어 나갔다.
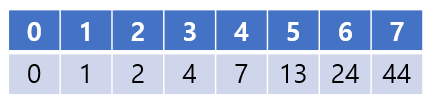
나의 답안
private static int solution(int n) {
int[] dp = new int[n + 1];
dp[1] = 1;
if (n >= 2) {
dp[2] = 2;
}
if (n >= 3) {
dp[3] = 4;
}
for (int i = 4; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3];
}
return dp[n];
}'BackJoon > Algorithm' 카테고리의 다른 글
| (1780) 종이의 개수 (0) | 2023.04.09 |
|---|---|
| (2775) 부녀회장이 될테야 (0) | 2023.04.08 |
| (1463) 1로 만들기 (0) | 2023.04.08 |
| (2839) 설탕 배달 (0) | 2023.04.07 |
| (11047) 동전 (0) | 2023.04.03 |

